Puzzle #8: Pentominoes : TurkZeka

A pentomino, if you don't know, is a group of five squares joined together along the edges.
It's possible to build 12 pentominoes only, not counting rotations and flips.
They are named: F, I, L, P, N, T, U, V, W, X, Y, Z.

The container above is a rectangular box 10 x 6 (really 12 x 5 = 10x 6).
There are 2,339 different way to put the twelve pentominoes in a container like this box.

How many different way to put twelve pentominoes in a same container (10x6) according to both of rules below?

Rule 1: T and Z should be located into same rows (rows 1,2,3 or rows 2,3,4 or rows 3,4,5 or rows 4,5,6)
(T is in the rows 1,2,3 and Z is in the rows 3,4,5 at the sample container above.
Namely, they aren't at the same rows.These placement doesn't fit this rule.)

Rule 2: T should hold a place left to Z. (TZ is valid but ZT is not.)
(The sample container above fits this rule.)

Three samples to show placement T and Z only :

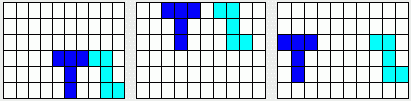
You can not rotate or reflect the T and Z. T and Z should be located like shown at the samples.

A valid full placement :

Click here for displaying the point list of the last week.)