ペントミノとは,5つの正方形を辺でつなげたものの集まりのことです.
回転や反転を除くと,全部で12個のペントミノを組み立てることが可能です.
これらは次のように(アルファベットで)名づけられます.:
F, I, L, P, N, T, U, V, W, X, Y, Z.
上の入れ物は 10 x 6
の長方形型の箱です.(実際
12 x 5 = 10x 6)
この箱に12個のペントミノを収める異なった収め方は,全部で
2,339
通りあります.
では,下記のルールの両方に従って,同じ入れ物
(10x6)
に12個のペントミノを収める異なった収め方は全部で何通りあるでしょうか?
ルール1:
T
と Z
は同じ行に置かれるものとします.(1,2,3行目,2,3,4行目,3,4,5行目,4,5,6行目のどれか)
(上のサンプルでは,T
は1,2,3行目に,Z
は3,4,5行目にあります.
つまり,これらは同じ行にはなく,このルールを満たしていません.)
ルール2:
T
は
Z
よりも左に置かれるものとします.(TZ
はいいですが,ZT
はいけません.)
(上のサンプルはこのルールを満たしています.)
T
と Z
のみの配置の3つのサンプル
:
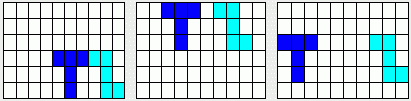
T
と
Z
は回転や反転を行なってはいけません.T
と
Z
はサンプルに見られるように置かれるものとします.
ある正しい全配置
:
(先週の得点リストを表示するには
ココ
をクリックして下さい.)