5 adet karenin
birleştirilmesiyle oluşturulabilecek farklı şekillerin hepsine pentomino denir.
Bir pentominonun döndürülmesi ve/veya ters çevrilmesi ile elde edilen şekiller
de aynı pentominodur ve birden fazla sayılmaz. Toplam 12 adet pentomino elde
edilebilir.
Her pentomino bir harfle gösterilir: F, I, L, P, N, T, U, V, W, X, Y, Z.
Yukarıdaki
tablo 10x6 boyutlarında bir dikdörtgendir. (12 pentomino x 5 = 10x 6).
12
adet pentominonun herbirini bir kez kullanarak tam
2,339 adet farklı yerleştirme ile 10x6 boyutlarında dikdörtgenler oluşturulabilir.
Sizden istenen
ise, aşağıdaki 2 kuralın ikisine birden uyarak ve 12 pentominonun herbirini bir kez
kullanarak kaç farklı yerleşime sahip 10x6 boyutlarında dikdörtgen oluşturulabileceğini bulmanız.
Kural 1:
T ve Z aynı satırlar üzerinde olmalıdır. (1., 2., 3. satırlar veya 2.,
3., 4. satırlar veya 3., 4., 5. satırlar veya 4., 5., 6.satırlarda.)
(Yukarıdaki örnek
tabloda, T 1.,2. ve 3. satırlarda, Z ise 3. ,4. ve 5. satırlarda yer
alıyor. Yani farklı satırlardalar. Bu yerleşim bu kurala uymuyor.)
Kural 2:
T mutlaka Z'nin solunda yer almalıdır. (TZ doğru,
ZT ise yanlış bir yerleşimdir.)
(Yukarıdaki örnek tablo bu kurala
uyuyor.)
Sadece T ve Z'nin
yerleşimlerini göstermek için 3 örnek:
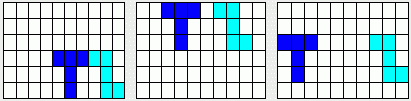
T ve Z'yi yan veya ters çevirmek (ayna görüntüsü) kabul edilmemektedir.
Örneklerde gösterildiği şekilde konumlandırılmalıdır.
Geçerli bir tam yerleşim: